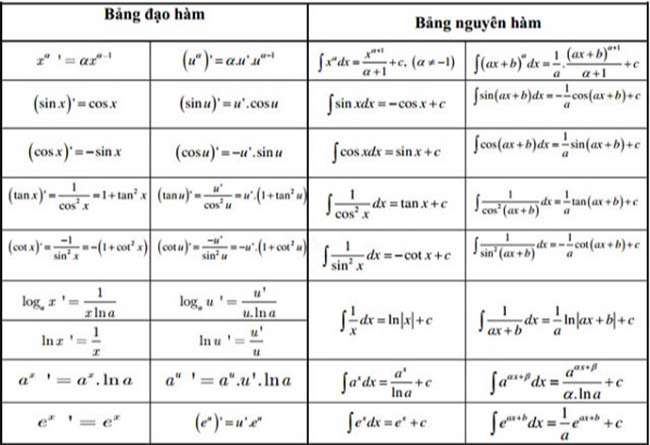
Bảng đầy đủ các công thức đạo hàm và đạo hàm lượng giác
Bài này Trung tâm gia sư Tâm Tài Đức xin chia sẽ cho các bạn Bảng đầy đủ các công thức đạo hàm và đạo hàm lượng giác các công thức toán học khi không được luyện tập (giải bài tập nhiều) thì sẽ rất nhanh quên, cho bạn cầm bảng công thức học cả ngày sau một thời gian bạn không giải bài tập bản sẽ quên, ở công thức lượng giác hay các công thức đạo hàm và cả những công thức khác điều vậy cả?
Bài này gia sư Tâm Tài Đức chia sẽ những gì?
Full bảng công công thức đạo hàm, Đạo hàm của hàm lượng giác và các hàm lượng giác, công thức đạo hàm cao cấp. Chúng ta cùng xem nào?
Bạn đang xem: CÔNG THỨC ĐẠO HÀM
Đạo hàm trong giải tích, hàm số thực.
Trong giải tích toán học, đạo hàm của một hàm số thực chất là sự mô tả sự biến thiên của hàm số tại một điểm nào đó. Cùng với tích phân (một phép toán ngược lại), đạo hàm là một trong hai khái niệm cơ bản trong giải tích.
Đạo hàm trong hình học là gì ?
Đạo hàm có biểu diễn trong hình học là hệ số góc của tiếp tuyến với đồ thị biểu diễn hàm số. Về vật lý, đạo hàm biểu diễn vận tốc tức thời của một chất điểm chuyển động hoặc cường độ dòng điện tức thời tại một điểm trên dây dẫn.
Định nghĩa đạo hàm

Đạo hàm và công thức đạo hàm cần biết

Công thức đạo hàm lượng giác

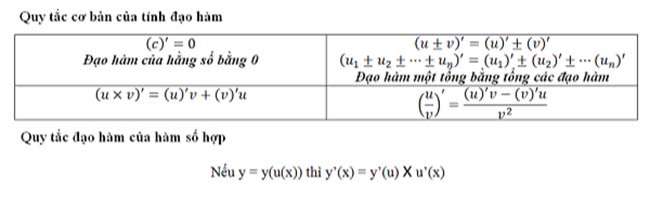
Quy tắc cơ bản của đạo hàm
- Quy tắc cơ bản của tính đạo hàm
- Quy tắc đạo hàm của hàm số hợp
Công thức đạo hàm cơ bản
- Đạo hàm của f(x) với x là biến số
- Đạo hàm của f(u) với u là một hàm số
- Đạo hàm của một số phân thức hữu tỉ thường gặp

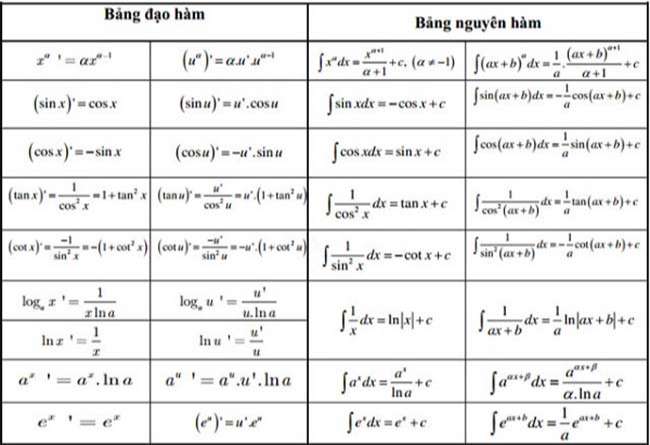
Bảng đạo hàm và nguyên hàm
- Bảng đạo hàm
- Bảng nguyên hàm
Tính đạo hàm bằng máy tính như thế nào?
Máy tính cầm tay là một công cụ đắc lực trong việc tính đạo hàm cấp 1, cấp 2. Tính đạo hàm bằng máy tính mang lại kết quả có độ chính xác cao và các thao tác thực hiện rất dễ dàng như sau:
Tính đạo hàm cấp 1:
Tính đạo hàm cấp 2:
Dự đoán công thức đạo hàm bậc n :
+ Bước 1: Tính đạo hàm cấp 1, đạo hàm cấp 2, đạo hàm cấp 3.
+ Bước 2: Tìm quy luật về số, quy luật về dấu, về hệ số, về biến số, về số mũ rồi rút ra công thức tổng quát

Đạo hàm cấp cao
Giả sử hàm số y = f(x) có đạo hàm f'(x)
Đạo hàm của hàm số f'(x), nếu có, được gọi là đạo hàm cấp hai của hàm số f(x), kí hiệu là y” hay f”(x).
Đạo hàm của hàm số f”(x), nếu có, được gọi là đạo hàm cấp ba của hàm số f(x), kí hiệu là y”’ hay f”'(x).
Tương tự, đạo hàm của đạo hàm cấp (n-1) được gọi là đạo hàm cấp n của hàm số y = f(x), kí hiệu là y(n)hay f(n)(x).
f(n)(x)=[f(n−1)(x)]′f(n)(x)=[f(n−1)(x)]′ , với n thuộc Z và n >= 2
Bảng đạo hàm cấp cao đầy đủ và công thức Lepnit:

Đăng bởi: THPT Sóc Trăng
Chuyên mục: Giáo dục