Hướng dẫn giải bài tập, bài thực hành trong bài 11: Phương pháp giải một số bài toán về toàn mạch – sách giáo khoa vật lí 11. Tất cả các kiến thức lý thuyết và bài tập trong bài học này đều được giải đáp cẩn thận, chi tiết. Chúng ta tham khảo để học tốt vật lí 11 bài 11: Phương pháp giải một số bài toán về toàn mạch nhé.
Câu trả lời:
I. TÓM TẮT LÝ THUYẾT
1. Kiến thức trọng tâm
Toàn mạch: mạch điện gồm nguồn điện có suất điện động $varepsilon $ và điện trở trong r hoặc gồm các nguồn điện được ghép thành bộ.
Mạch ngoài gồm các điện trở hoặc các vật dẫn được coi như điện trở nối liền hai cực của nguồn điện.
Định luật Ôm cho toàn mạch: Cường độ dòng điện chạy trong mạch kín tỉ lệ thuận với suất điện động của nguồn điện và tỉ lệ nghich với điện trở toàn phần của mạch đó.
$I = frac{varepsilon }{R_{N} + r}$.
Các công thức cần nhớ:
$I = frac{varepsilon }{R_{N} + r}$ (A).
$varepsilon = I.(R_{N} + r)$ (V).
$U = I.R_{N} = varepsilon – I.r$ (V).
$A_{ng} = varepsilon .I.t$. (J).
$P_{ng} = varepsilon .I$ (W).
$A = U.I.t$ (J).
$P = U.I$. (W).
$H = frac{U_{N}}{varepsilon } = frac{R_{N}}{R_{N} + r}$ (%)
2. Phương pháp
B1: Phân tích cấu tạo của mạch, xem mạch mắc nối tiếp? Hay song song? Vẽ sơ đồ mạch điện.
B2: Tính các điện trở tương đương của mạch.
B3: Áp dụng định luật Ôm để tính cường độ dòng điện trong mạch.
B4: Tính các tham số còn lại của bài toán và kết luận.
II. Bài tập áp dụng
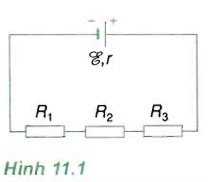
Bài tập 1: Một mạch điện có sơ đồ như hình…
Một mạch điện có sơ đồ như hình 11.1, trong đó nguồn điện có suất điện động $varepsilon = 6$ (V) và điện trở trong r = 2 $Omega $, các điện trở R1 = 5 $Omega $, R2 = 10 $Omega $ và R3 = 3 $Omega $.
a. Tính điện trở RN của mạch ngoài.
b. Tính cường độ dòng điện I chạy qua nguồn điện và hiệu điện thế mạch ngoài U.
c. Tính hiệu điện thế U1 giữa hai đầu điện trở R1.

Hướng dẫn giải:
Mạch gồm R1 nt R2 nt R3;
a. Điện trở của mạch ngoài là: RN = R1 + R2 + R3 = 5 + 10 + 3 = 18 $Omega $.
b. Áp dụng định luật Ôm cho toàn mạch, ta có:
Cường độ dòng điện chạy qua nguồn điện là: $I = frac{varepsilon }{R_{N} + r} = frac{6}{2 + 18} = 0,3$ (A).
Hiệu điện thế mạch ngoài là: $U = I.R_{N} = 0,3.18 = 5,4$ (V).
c. Hiệu điện thế giữa hai đầu điện trở R1 là: U1 = I.R1 = 0,3.5 = 1,5 (V).
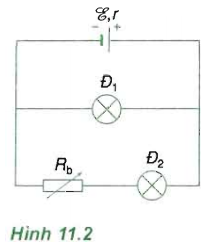
Bài tập 2: Một mạch điện có sơ đồ như Hình 11.2…
Một mạch điện có sơ đồ như Hình 11.2, trong đó nguồn điện có suất điện động $varepsilon = 12,5$ (V) và có điện trở trong r = 0,4 $Omega $; bóng đèn Đ1 có ghi số 12 V – 6 W; bóng đèn Đ2 loại 6 V – 4,5 W; Rb là một biến trở.
a. Chứng tỏ rằng khi điều chỉnh biến trở Rb có trị số là 8 $Omega $ thì các đèn Đ1 và Đ2 sáng bình thường.
b. Tính công suất Png và hiệu suất H của nguồn khi đó.
Hướng dẫn giải:
Mạch gồm Đ1 // (Rb nt Đ2).
a. Điện trở của mỗi đèn là:
$R_{Đ1} = frac{U^{2}_{Đ_{1}}}{P_{1}} = frac{12^{2}}{6} = 24$ $Omega $.
$R_{Đ2} = frac{U^{2}_{Đ_{2}}}{P_{2}} = frac{6^{2}}{4,5} = 8$ $Omega $.
Khi Rb = 8 $Omega $ thì điện trở tương đương của mạch là:
R2b = R2 + Rb = 8 + 8 = 16 $Omega $.
$frac{1}{R_{N}} = frac{1}{R_{1}} + frac{1}{R_{2b}} = frac{1}{24} + frac{1}{16} = frac{5}{48}$
$Rightarrow $ $R_{N} = 9,6$ $Omega $.
Cường độ dòng điện trong mạch chính là: $I = frac{varepsilon }{R_{n} + r} = frac{12,5}{9,6 + 0,4} = 1,25$ (A).
Hiệu điện thế mạch ngoài là: UN = I.RN = 1,25.9,6 = 12 (V).
Cường độ dòng điện trong mỗi nhánh là:
$I_{1} = frac{U_{N}}{R_{1} = frac{12}{24} = 0,5}$ (A).
$I_{2b} = frac{U_{N}}{R_{2b} = frac{12}{16} = 0,75}$ (A).
Cường độ dòng điện qua mỗi đèn là:
IĐ1 = I1 = 0,5 (A). (1)
IĐ2 = I2b = 0,75 (A). (2)
Cường độ dòng điện định mức qua mỗi đèn là:
$I_{đm1} = frac{U_{Đ1}}{R_{Đ1}} = frac{12}{24} = 0,5$ (A). (3)
$I_{đm2} = frac{U_{Đ2}}{R_{Đ2}} = frac{6}{8} = 0,75$ (A). (4)
Từ (1), (2), (3) và (4), ta có: Dòng điện chạy qua mỗi bóng đèn đúng bằng dòng điện định mức của mỗi bóng, do đó các đèn sáng bình thường.
b. Công suất của nguồn là: $P_{ng} = varepsilon .I = 12,5.1,25 = 15,625$ (W).
Hiệu suất của nguồn là: $H = frac{U_{N}}{varepsilon } = frac{12}{12,5} = 96$ (%).
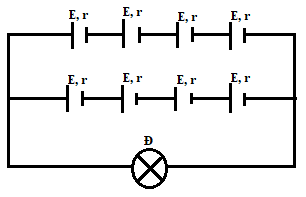
Bài tập 3: Có tám nguồn điện cùng loại vớ….
Có tám nguồn điện cùng loại với cùng suất điện động $varepsilon = 1,5$ (V) và điện trở trong r = 1 $Omega $. Mắc các nguồn này thành bộ hỗn hợp đối xứng gồm hai dãy song song để thắp sáng bóng đèn 6 V – 6 W. Coi rằng bóng đèn có điện trở như khi sáng bình thường.
a. Vẽ sơ đò mạch điện kín gồm bộ nguồn và bóng đèn mạch ngoài.
b. Tính cường độ I của dòng điện thực sự chạy qua bóng đèn và công suất điện Pđ của bóng đèn khi đó.
c. Tính công suất Png của bộ nguồn, công suất Pi của mối nguồn trong bộ và hiệu điện thế Ui giữa hai cực của mỗi nguồn đó.
Hướng dẫn giải:
a. Mạch gồm hai dãy mắc song song, mỗi dãy gồm có 4 nguồn điện mắc nối tiếp.
Sơ đồ mạch điện:
b. Suất điện động của bộ nguồn là: $varepsilon _{b} = 4varepsilon = 4.1,5 = 6$ (V).
Điện trở trong của bộ nguồn điện: $r_{b} = frac{4.r}{2} = frac{4.1}{2} = $ $Omega $.
Điện trở của bóng đèn là: $R = frac{U^{2}_{đ}}{P_{đ}} = frac{6^{2}}{6} = 6$ (V).
Áp dụng định luật Ôm cho toàn mạch, ta có cường độ dòng điện chạy qua đèn là:
$I = frac{varepsilon _{b}}{R + r} = frac{6}{6 + 2} = 0,75$ (A).
Công suất của bóng đèn là: P = I2.R = (0,75)2.6 = 3,375 (W).
c. Công suất của bộ nguồn là: $P_{ng} = varepsilon .I = 6.0,75 = 4,5$ (W).
Công suất của mỗi nguồn là Pi = 0,5625 W.
Hiệu điện thế giữa hai đầu nguồn là: Ui = 1,125 V.
III. GIẢI BÀI TẬP
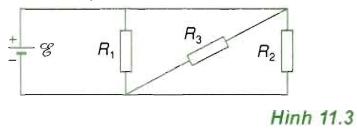
Giải câu 1: Cho mạch điện có sơ đồ như Hình…
Cho mạch điện có sơ đồ như Hình 11.3, trong đó nguồn điện có suất điện động $varepsilon = 6$ (V) và có điện trở trong không đáng kể. Các điện trở R1 = R2 = 30 $Omega $; R3 = 7,5 $Omega $.
a. Tính điện trở tương đương của mạch ngoài
b. Tính cường độ dòng điện chạy qua mỗi điện trở mạch ngoài.
Bài giải:
a. Mạch gồm: R1 // R2 // R3
Điện trở tương đương của mạch ngoài là:
$frac{1}{R_{N}} = frac{1}{R_{1}} + frac{1}{R_{2}} + frac{1}{R_{3}} = frac{1}{30} + frac{1}{30} + frac{1}{7,5} = frac{1}{5}$ $Omega $.
$Rightarrow $ $R_{N} = 5$ $Omega $.
b. Cường độ dòng điện trong mạch chính là:
$I = frac{varepsilon }{R_{N} + r} = frac{6}{5 + 0} = 1.2$ (A).
Ta có: I = I1 + I2 + I3 và I.RN = I1.R1 = I2.R2 = I3.R3 $Rightarrow $ I1 = I2 = 0,2 (A); I3 = 0,8 (A).
Giải câu 2: Cho mạch điện có sơ đồ như Hình…
Cho mạch điện có sơ đồ như Hình 11.4, trong đó các acquy có suất điện động $varepsilon _{1} = 12$ (V); $varepsilon _{2} = 6$ (V) và điện trở trong không đáng kể. Các điện trở R1 = 4 $Omega $; R2 = 8 $Omega $.
a. Tính cường độ dòng điện chạy qua mạch.
b. Tính công suất tiêu thụ của mỗi điện trở.
c. Tính công suất của mỗi acquy và năng lượng mà mỗi acquy cung cấp trong 5 phút.
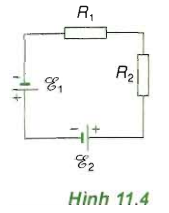
Bài giải:
Mạch gồm R1 nt R2 và hai nguồn mắc nối tiếp.
a. Điện trở tương đương của mạch: RN = R1 + R2 = 4 + 8 = 12 $Omega $.
Suất điện động của bộ nguồn là: $varepsilon _{b} = varepsilon _{1} + varepsilon _{2} = 12 + 6 = 18$ (V).
Cường độ dòng điện trong mạch là: $I = frac{varepsilon _{b}}{R_{N} + r} = frac{18}{12 + 0} = 1.5$ (A).
b. Công suất tiêu thụ của mỗi điện trở là:
$P_{R1} = I_{1}^{2}.R_{1} = I^{2}.R_{1} = 1,5^{2}.4 = 9$ (W).
$P_{R2} = I_{2}^{2}.R_{2} = I^{2}.R_{2} = 1,5^{2}.8 = 18$ (W).
(Vì do mắc nối tiếp nên có: I1 = I2 = I).
c. Công suất của mỗi acquy là:
$P_{ng1} = varepsilon _{1}.I_{1} = 12.1,5 = 18$ (W).
$P_{ng2} = varepsilon _{2}.I_{1} = 6.1,5 = 9$ (W).
Năng lượng mà mỗi acquy cung cấp trong 5 phút là:
A1 = Png1.t = 18.5.60 = 5400 J.
A2 = Png2.t = 9.5.60 = 2700 J.
Giải câu 3*: Cho mạch điện có sơ đồ như Hình…
Cho mạch điện có sơ đồ như Hình 11.5, trong đó nguồn điện có suất điện động $varepsilon = 12$ (V) và điện trở trong r = 1,1 $Omega $; điện trở R = 0,1 $Omega $.
a. Điện trở x phải có trị số là bao nhiêu để công suất tiêu thụ ở mạch ngoài là lớn nhất?
b. Điện trở x phải có trị số là bao nhiêu để công suất tiêu thụ ở điện trở này là lớn nhất? Tính công suất lớn nhất đó.
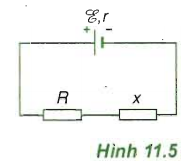
Bài giải:
Mạch gồm hai điện trở mắc nối tiếp.
Điện trở tương đương của mạch là: RN = R + x $Omega $.
Cường độ dòng điện trong mạch là: $I = frac{varepsilon }{R_{N} + r} = frac{varepsilon }{R + x +r}$ (A).
a. Công suất tiêu thụ của mạch ngoài là:
$P = I^{2}.R_{N} = (frac{varepsilon }{R + x +r})^{2}.(R + x) = frac{varepsilon ^{2}}{(R + x) + frac{r^{2}}{R + x} + 2.r}$ (W).
Để P max thì $frac{varepsilon ^{2}}{(R + x) + frac{r^{2}}{R + x} + 2.r}$ max hay mẫu số phải min.
$(R + x) + frac{r^{2}}{R + x} + 2.r$ min khi $(R + x) + frac{r^{2}}{R + x}$ min.
Áp dụng bất đẳng thức Cosi cho hai số dương, ta có mẫu số min khi R + x = r hay x = r – R = 1,1 – 0,1 = 1 $Omega $.
b. Công suất tiêu thụ trên biến trở x là:
$P_{x} = I_{x}^{2}.x = I^{2}.x = (frac{varepsilon }{R + x +r})^{2}.x = frac{varepsilon ^{2}}{frac{(R + r)^{2}}{x} + 2.(R + r) + x}$ (W).
Công suất tiêu thụ trên biến trở là lớn nhất khi mẫu số max.
Mẫu số max khi x = R + r =1,1 + 0,1 = 1,2 $Omega $. (Sử dụng bất đẳng thức Cosi để đánh giá).