
Bất đẳng thức và các ứng dụng
I. Khái niệm bất đẳng thức cơ bản
1.1 Số thức dương, số thực âm
Nếu a là số thực dương, ta kí hiệu a>0
Nếu a là số thực âm, ta kí hiệu a
Bạn đang xem: Công thức bất đẳng thức
Nếu a là số thực dương hoặc a = 0, ta nói a là số thực không âm, kí hiệu a≥0a≥0
Nếu a là số thực âm hoặc a = 0, ta nói a là số thực không dương, kí hiệu a≤0a≤0
Chú ý: Với hai số thực a, b chỉ có một trong ba khả năng sau xảy ra:
a>b hoặc a
Phủ định của mệnh đề a>0 là a≤0a≤0
Phủ định của mệnh đề a


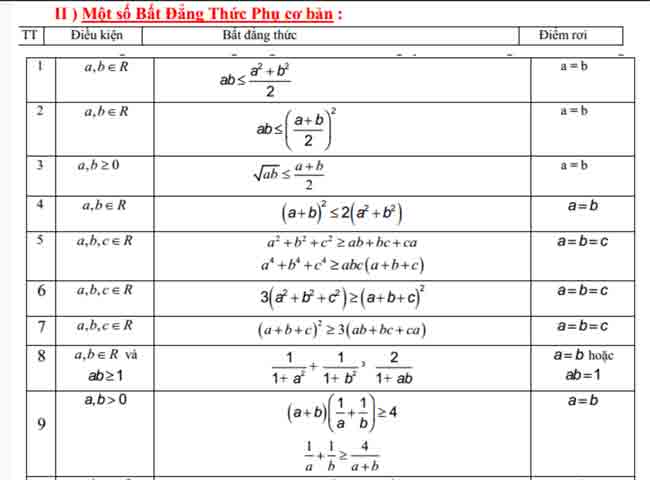




















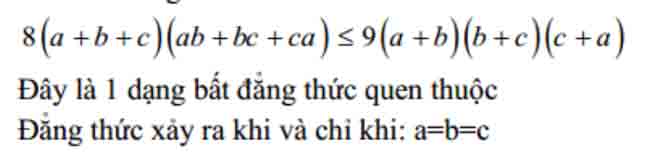
Bất đẳng thức có được từ hằng đẳng thức dạng (a−b)2≥0



Bất đẳng thức AM – GM (Sách giáo khoa việt nam gọi là bất đẳng thức Côsi)







Bất đẳng thức Cauchy – Schwarz (Sách giáo khoa việt nam gọi là bất đẳng thức Bunhiacopsky)





Bất đẳng thức Cauchy – Schwarz dạng phân thức



Bất đẳng thức Mincopski (bất đẳng thức véctơ)


Bài 1. Cho các số thực dương a, b, c thỏa mãn a2 + b2 + c2 = 3.
Chứng minh rằng:


Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.
Ôn tập về Bất đẳng thức
1. Khái niệm bất đẳng thức
– Các mệnh đề dạng “ab” được gọi là bất đẳng thức.
2. Bất đẳng thức hệ quả và bất đẳng thức tương đương
– Nếu mệnh đề “a
– Nếu bất đẳng thức a
3. Tính chất của bất đẳng thức
° Cộng hai vế của bất đẳng thức với một số:
a
° Nhân hai vế của bất đẳng thức với một số:
– Với c>0: a
– Với c bc
° Cộng hai bất đẳng thức cùng chiều
a
° Nhân hai bất đẳng thức cùng chiều
– Với a>0, c>0: a
° Nâng hai vế của bất đẳng thức lên một lũy thừa
– Với n ∈ N*: a2n+1 2n+1
– Với n ∈ N* và a>0: a2n 2n
° Khai căn hai vế của một bất đẳng thức

2. Các hệ quả của Bất đẳng thứ Cô-si
° Hệ quả 1: Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.

Bất đẳng thức chứa dấu trị tuyệt đối
Từ định nghĩa giá trị tuyệt đối, ta có tính chất bất đẳng thức trị tuyệt đối như sau
° |x| ≥ 0, |x| ≥ x, |x| ≥ -x
° Với a>0:
|x| ≤ 0 ⇔ -a ≤ x ≤ a
|x| ≥ a ⇔ x ≤ -a hoặc x ≥ a
° |a| – |b| ≤ |a + b| ≤ |a| + |b|
Bài tập vận dụng Bất đẳng thức
* Bài 1 trang 79 SGK Đại Số 10: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x?
a) 8x > 4x ; b) 4x > 8x
c) 8x2 > 4x2 ; d) 8 + x > 4 + x
* Lời giải:
– Đáp án đúng: d) 8 + x > 4 + x
– Vì 8 > 4 nên với mọi x thì 8+ x > 4+ x ( tính chất cộng hai vế của BĐT với 1 số). Nên khẳng định d là đúng với mọi giá trị của x.
+ Các đáp án khác sai vì:
a) Ta có: 8 > 4 nên để 8x > 4x thì x > 0
– Do đó, chỉ đúng khi x > 0 (hay nói cách khác nếu x
b) Ta có: 4 8x thì x
– Do đó, khẳng định chỉ đúng khi x
c) chỉ đúng khi x ≠ 0
Bài 2 trang 79 SGK Đại Số 10: Cho số x > 5, số nào trong các số sau đây là số nhỏ nhất?
A=5/x; B=5/x + 1; C = 5/x – 1; D = x/5.
* Lời giải:
– Với mọi x ≠ 0 ta luôn có: – 1

→ Vậy ta có C
* Bài 3 trang 79 SGK Đại Số 10: Cho a, b, c là độ dài ba cạnh của một tam giác.
1) Chứng minh (b – c)2 2
2) Từ đó suy ra: a2 + b2 + c2
* Lời giải:
1) (b – c)2 2
– Vì a, b, c là độ dài 3 cạnh của một tam giác nên tổng 2 cạnh luôn lớn hơn cạnh còn lại. ⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
– Ta có: (b – c)2 – a2 = (b – c – a)(b – c + a)
Do b c ⇒ b + a – c > 0.
Suy ra: (b – c – a)(b – c + a) 2 – a2 2 2
2) Từ kết quả câu 1) ta có
a2 > (b – c)2
b2 > (a – c)2
c2 > (a – b)2
– Cộng vế với vế ba bất đẳng thức trên ta có:
a2 + b2 + c2 > (b – c)2 + (c – a)2 + (a – b)2
⇒ a2 + b2 + c2 > b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2
⇒ a2 + b2 + c2 > 2(a2 + b2 + c2) – 2(ab + bc + ca)
⇒ a2 + b2 + c2
Bài 4 trang 79 SGK Đại Số 10: Chứng minh rằng: x3 + y3 ≥ x2y + xy2, ∀x, y ≥ 0
* Lời giải:
Với x ≥ 0; y ≥ 0 thì x + y ≥ 0
Ta có: x3 + y3 ≥ x2y + xy2
⇔ (x3 + y3) – (x2y + xy2) ≥ 0
⇔ (x + y)(x2 – xy + y2) – xy(x + y) ≥ 0
⇔ (x + y)(x2 – xy + y2 – xy) ≥ 0
⇔ (x + y)(x2 – 2xy + y2) ≥ 0
⇔ (x + y)(x – y)2 ≥ 0 (Luôn đúng vì x + y ≥ 0 ; (x – y)2 ≥ 0)
Dấu “=” xảy ra khi (x – y)2 = 0 ⇔ x = y.
* Bài 5 trang 79 SGK Đại Số 10: Chứng minh rằng:
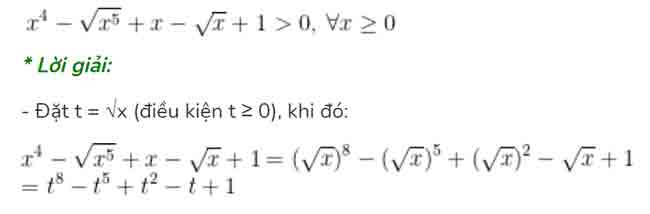
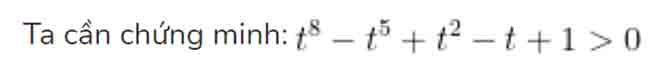
+ Xét 0 ≤ t 3 3 > 0 ; 1 – t > 0
t8 – t5 + t2 – t + 1 = t8 + (t2 – t5) + (1 – t) = t8 + t2.(1 – t3) + (1 – t) > 0 + 0 + 0 = 0
(vì t8 ≥ 0; t2 ≥ 0 ⇒ t2(1 – t3) ≥ 0)
+ Xét t ≥ 1 ⇒ t3 ≥ 1 ⇒ t3 – 1 ≥ 0 và t – 1 ≥ 0.
t8 – t5 + t2 – t + 1 = t5.(t3 – 1) + t.(t – 1) + 1 ≥ 0 + 0 + 1 > 0
Vậy với mọi t ≥ 0 thì t8 – t5 + t2 – t + 1 ≥ 1/2 > 0 hay
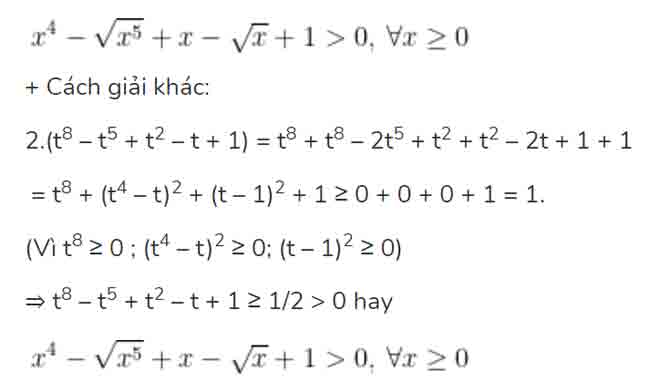
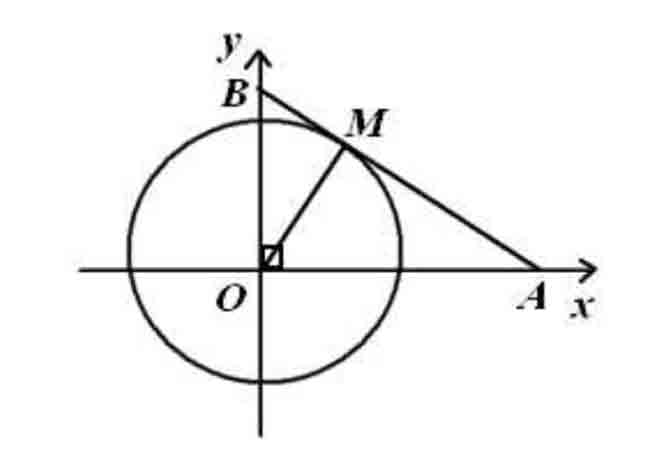
Bài 6 trang 79 SGK Đại Số 10: Trong mặt phẳng tọa độ Oxy, trên các tia Ox và Oy lần lượt lấy các điểm A và B thay đổi sao cho đường thẳng AB luôn tiếp xúc với đường tròn tâm O bán kính 1. Xác định tọa độ của A và B để đoạn AB có độ dài nhỏ nhất.
Lời giải:
– Gọi tiếp điểm của AB và đường tròn tâm O, bán kính 1 là M, ta có: OM ⊥ AB.
Áp dụng bất đẳng thức Cô-si ta có:
MA + MB ≥ 2√MA.MB = 2. √1 = 2
Dấu « = » xảy ra khi MA = MB = 1.
Khi đó OA = √(MA2 + MO2) = √2 ; OB = √(OM2 + MB2) = √2.
Mà A, B nằm trên tia Ox và Oy nên A(√2; 0); B(0; √2)
Vậy tọa độ là A(√2, 0) và B(0, √2).
Đăng bởi: THPT Sóc Trăng
Chuyên mục: Giáo dục