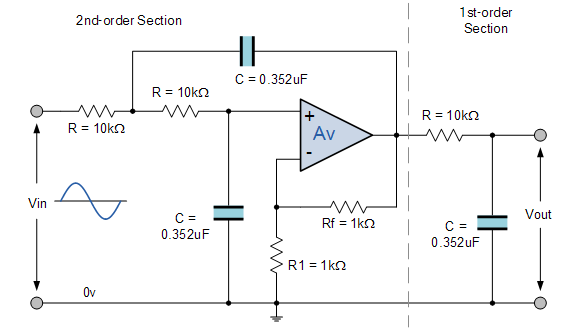
Thiết kế bộ lọc Butterworth : Trong các ứng dụng sử dụng bộ lọc để định hình phổ tần số của tín hiệu chẳng hạn như trong hệ thống truyền thông hoặc điều khiển, hình dạng hoặc chiều rộng của độ dốc tín hiêuh còn được gọi là “dải chuyển tiếp”, đối với bộ lọc bậc một đơn giản có thể quá dài hoặc rộng và các bộ lọc hoạt động được thiết kế với nhiều hơn một “đơn hàng” là bắt buộc. Những loại bộ lọc này thường được gọi là bộ lọc “bậc cao” hoặc “n th -order” .
Độ phức tạp hoặc loại bộ lọc được xác định bởi “thứ tự” của bộ lọc và phụ thuộc vào số lượng các thành phần phản kháng như tụ điện hoặc cuộn cảm trong thiết kế của nó. Chúng tôi cũng biết rằng độ dốc và do đó độ rộng của dải chuyển tiếp, phụ thuộc vào số thứ tự của bộ lọc và đối với bộ lọc bậc một đơn giản,độ dốc tiêu chuẩn là 20dB / decade hoặc 6dB / octave.
Sau đó, đối với bộ lọc có “n th -order” , nó sẽ có độ dốc tần số tiếp theo là 20n dB / decade hoặc 6n dB / octave. Vì vậy, bộ lọc bậc nhất có độ dốc là 20dB / decade (6dB / octave), bộ lọc bậc hai có độ dốc tín hiệu là 40dB / decade (12dB / octave) và bộ lọc bậc bốn có đọ dốc tín hiệu 80dB / decade (24dB /octave), v.v.
Bộ lọc bậc cao, chẳng hạn như bậc ba, bậc 4 và bậc 5 thường được hình thành bằng cách xếp tầng các bộ lọc bậc nhất và bậc hai với nhau.
Ví dụ: hai bộ lọc thông thấp bậc hai có thể được xếp tầng với nhau để tạo ra bộ lọc thông thấp bậc bốn, v.v. Mặc dù không có giới hạn đối với thứ tự của bộ lọc có thể được hình thành, khi thứ tự tăng lên thì kích thước và chi phí của nó cũng giảm, độ chính xác của nó cũng giảm.
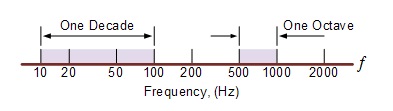
Decade và Octave
Một nhận xét cuối cùng về decade và octave . Trên thang tần số, decade là sự tăng lên mười lần (nhân với 10) hoặc giảm đi mười lần (chia cho 10). Ví dụ: 2 đến 20Hz đại diện cho một decade, trong khi 50 đến 5000Hz đại diện cho hai decade (50 đến 500Hz và sau đó là 500 đến 5000Hz).
Một octave là sự nhân đôi (nhân với 2) hoặc giảm một nửa (chia cho 2) của thang tần số. Ví dụ: 10 đến 20Hz đại diện cho một octave, trong khi 2 đến 16Hz là ba octave (2 đến 4, 4 đến 8 và cuối cùng là 8 đến 16Hz) nhân đôi tần số mỗi lần. Dù bằng cách nào, thang đo Logarit được sử dụng rộng rãi trong miền tần số để biểu thị giá trị tần số khi làm việc với bộ khuếch đại và bộ lọc, vì vậy điều quan trọng là phải hiểu chúng.
Thang tần số lôgarit
Vì các điện trở xác định tần số đều bằng nhau, và các tụ điện xác định tần số cũng vậy, nên tần số cắt hoặc tần số góc ( ƒ C ) đối với bộ lọc bậc nhất, bậc 2, bậc ba hoặc thậm chí là bộ lọc bậc bốn cũng phải bằng nhau và được tìm thấy bằng cách sử dụng phương trình quen thuộc bây giờ của chúng tôi:
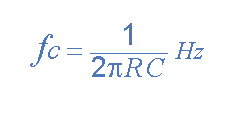
Cũng như bộ lọc bậc một và bậc hai, bộ lọc thông cao bậc ba và bậc bốn được hình thành bằng cách hoán đổi vị trí của các thành phần xác định tần số (điện trở và tụ điện) trong bộ lọc thông thấp tương đương. Bộ lọc bậc cao có thể được thiết kế bằng cách làm theo các quy trình mà chúng ta đã thấy trước đây trong hướng dẫn bộ lọc Thông thấp và Bộ lọc thông cao. Tuy nhiên, độ lợi tổng thể của các bộ lọc bậc cao là cố định vì tất cả các thành phần xác định tần số đều bằng nhau.
Lọc Xấp xỉ
Cho đến nay, chúng ta đã xem xét các mạch lọc bậc nhất thông thấp và thông cao, các đáp ứng pha và tần số kết quả của chúng. Một bộ lọc lý tưởng sẽ cung cấp cho chúng ta các thông số kỹ thuật về độ lợi dải thông và độ phẳng dải thông tối đa, suy giảm dải dừng(cấm dải) tối thiểu và cũng có bandwidth rất dốc để dừng dải dốc tín hiệu (dải chuyển tiếp) và do đó rõ ràng là một số lượng lớn phản hồi sẽ thỏa mãn các yêu cầu này.
Không ngạc nhiên khi có một số “hàm xấp xỉ” trong thiết kế bộ lọc tương tự tuyến tính sử dụng phương pháp toán học để xấp xỉ tốt nhất hàm truyền mà chúng ta yêu cầu đối với thiết kế bộ lọc.
Những thiết kế như vậy được biết đến như Elliptical , Butterworth , Chebyshev , Bessel , Cauer cũng như nhiều loại khác. Trong số năm chức năng xấp xỉ của bộ lọc tương tự tuyến tính “cổ điển” này, chỉ có Bộ lọc Butterworth và đặc biệt là thiết kế bộ lọc Butterworth thông thấp sẽ được coi là chức năng được sử dụng phổ biến nhất ở đây.
Thiết kế bộ lọc Butterworth thông thấp
Đáp ứng tần số của hàm xấp xỉ Bộ lọc Butterworth cũng thường được gọi là đáp ứng “phẳng cực đại” (không có gợn) vì dải tần được thiết kế để có đáp ứng tần số càng phẳng về mặt toán học từ 0Hz (DC) cho đến khi cắt – tần số tắt ở -3dB không có gợn sóng. Các tần số cao hơn ngoài điểm cắt sẽ giảm xuống 0 trong dải dừng ở 20dB / thập kỷ hoặc 6dB / quãng tám. Điều này là do nó có “hệ số chất lượng”, “Q” chỉ 0,707.
Tuy nhiên, một nhược điểm chính của bộ lọc Butterworth là nó đạt được độ bằng phẳng của dải thông này với chi phí của dải chuyển tiếp rộng khi bộ lọc thay đổi từ dải thông sang dải dừng. Nó cũng có đặc điểm kém pha. Đáp ứng tần số lý tưởng, được gọi là bộ lọc “bức tường gạch” và các giá trị xấp xỉ Butterworth tiêu chuẩn, cho các thứ tự bộ lọc khác nhau được đưa ra dưới đây.
Đáp ứng tần số lý tưởng cho thiết kế bộ lọc Butterworth
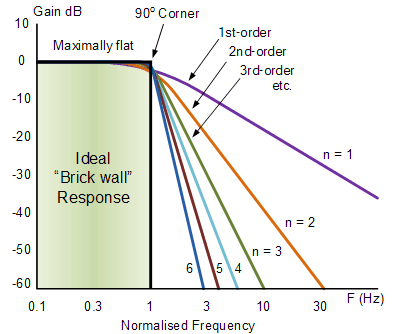
Lưu ý rằng thứ tự bộ lọc Butterworth càng cao, số lượng các giai đoạn xếp tầng có trong thiết kế bộ lọc càng cao và bộ lọc càng gần với phản hồi “bức tường gạch” lý tưởng.
Tuy nhiên, trong thực tế, đáp ứng tần số lý tưởng của Butterworth là không thể đạt được vì nó tạo ra gợn bandwidth quá mức.
Trong đó phương trình tổng quát đại diện cho bộ lọc Butterworth thứ tự “thứ n”, đáp ứng tần số được đưa ra là:
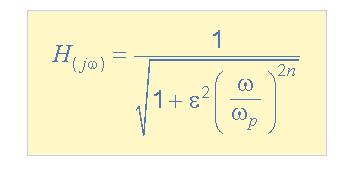
Trong đó: n đại diện cho thứ tự bộ lọc, Omega ω bằng 2πƒ và Epsilon ε là độ lợi bandwidth lớn nhất, (A max ). Nếu A max được xác định ở tần số bằng điểm góc -3dB cắt (ƒc), thì ε sẽ bằng một và do đó ε 2 cũng sẽ là một. Tuy nhiên, nếu bây giờ bạn muốn xác định A max ở một giá trị tăng điện áp khác, ví dụ 1dB hoặc 1,1220 (1dB = 20 * logA max ) thì giá trị mới của epsilon, ε được tìm thấy bằng:
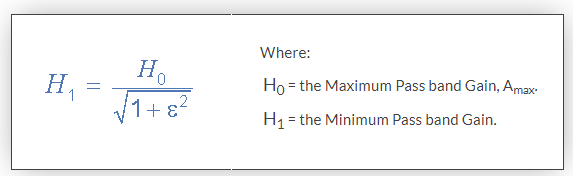
Hoán vị phương trình :
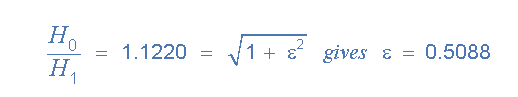Các đáp ứng tần số của một bộ lọc có thể được định nghĩa toán học của nó đáp ứng tần số với tiêu chuẩn H (jω) viết như sau:
Lưu ý: (jω) cũng có thể được viết thành (s) để biểu thị miền S. và hàm truyền kết quả cho bộ lọc thông thấp bậc hai được đưa ra như sau:
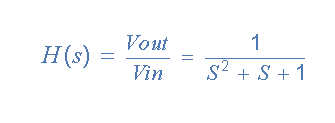
Để giúp đỡ trong việc thiết kế bộ lọc thông thấp của mình, Butterworth đã tạo ra các bảng tiêu chuẩn của đa thức thông thấp bậc hai chuẩn hóa với các giá trị của hệ số tương ứng với tần số góc cắt là 1 radian / giây.
| n | Normalised Denominator Polynomials in Factored Form |
| 1 | (1+s) |
| 2 | (1+1.414s+s2) |
| 3 | (1+s)(1+s+s2) |
| 4 | (1+0.765s+s2)(1+1.848s+s2) |
| 5 | (1+s)(1+0.618s+s2)(1+1.618s+s2) |
| 6 | (1+0.518s+s2)(1+1.414s+s2)(1+1.932s+s2) |
| 7 | (1+s)(1+0.445s+s2)(1+1.247s+s2)(1+1.802s+s2) |
| 8 | (1+0.390s+s2)(1+1.111s+s2)(1+1.663s+s2)(1+1.962s+s2) |
| 9 | (1+s)(1+0.347s+s2)(1+s+s2)(1+1.532s+s2)(1+1.879s+s2) |
| 10 | (1+0.313s+s2)(1+0.908s+s2)(1+1.414s+s2)(1+1.782s+s2)(1+1.975s+s2) |
Thiết kế bộ lọc Butterworth thông thấp
Tìm thứ tự của bộ lọc Butterworth thông thấp đang hoạt động có thông số kỹ thuật được đưa ra là: A max = 0,5dB ở tần số dải thông ( ωp ) là 200 radian / giây (31,8Hz) và A min = -20dB ở tần số dải dừng ( ωs ) là 800 radian / giây. Đồng thời thiết kế mạch lọc Butterworth phù hợp để đáp ứng các yêu cầu này.
Thứ nhất, độ lợi băng tần tối đa A max = 0,5dB bằng với độ lợi 1,0593 , hãy nhớ rằng: 0,5dB = 20 * log (A) ở tần số ( ωp ) 200 rads / s, vì vậy giá trị của epsilon ε được tìm thấy bởi:
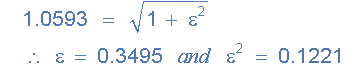
Thứ hai, độ lợi dải dừng tối thiểu A min = -20dB bằng với độ lợi 10 (-20dB = 20 * log (A)) ở tần số dải dừng ( ωs ) là 800 rads / s hoặc 127,3Hz.
Việc thay thế các giá trị vào phương trình tổng quát cho phản ứng tần số của bộ lọc Butterworth cho chúng ta những tính toán sau:
Vì n phải luôn là một số nguyên (số nguyên) nên giá trị cao nhất tiếp theo của 2,42 là n = 3 , do đó, “bộ lọc bậc ba là bắt buộc” và để tạo bộ lọc Butterworth bậc ba , giai đoạn bộ lọc bậc hai xếp tầng cùng với một giai đoạn lọc bậc nhất là bắt buộc.
Từ bảng Đa thức Butterworth thông thường được chuẩn hóa ở trên, hệ số cho bộ lọc bậc ba được cho là (1 + s) (1 + s + s 2 ) và điều này cho chúng ta mức tăng 3-A = 1 , hoặc A = 2 . Khi A = 1 + (Rf / R1) , việc chọn giá trị cho cả điện trở hồi tiếp Rf và điện trở R1 cho chúng ta các giá trị 1kΩ và 1kΩ tương ứng là: ( 1kΩ / 1kΩ) + 1 = 2 .
Chúng ta biết rằng tần số góc cắt, điểm -3dB ( ω o ) có thể được tìm thấy bằng công thức 1 / CR , nhưng chúng ta cần tìm ω o từ tần số băng tần ω p khi đó,
Vì vậy, tần số góc cắt được cho là 284 rads / s hoặc 45,2Hz, (284 / 2π) và sử dụng công thức quen thuộc 1 / CR, chúng ta có thể tìm thấy các giá trị của điện trở và tụ điện cho mạch bậc ba của chúng ta.
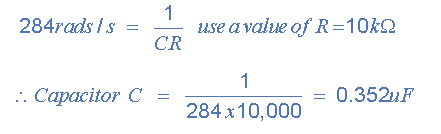
Lưu ý rằng giá trị ưu tiên gần nhất với 0,352uF sẽ là 0,36uF hoặc 360nF .
Bộ lọc thông thấp Butterworth bậc ba
và cuối cùng là mạch của chúng tôi về Bộ lọc Butterworth thông thấp bậc ba với tần số góc cắt 284 rads / s hoặc 45,2Hz, độ lợi dải thông tối đa là 0,5dB và độ lợi dải dừng tối thiểu là 20dB được xây dựng như sau.
Vì vậy, đối với Bộ lọc thông thấp Butterworth bậc 3 của chúng tôi với tần số góc là 45,2Hz, C = 360nF và R = 10kΩ.