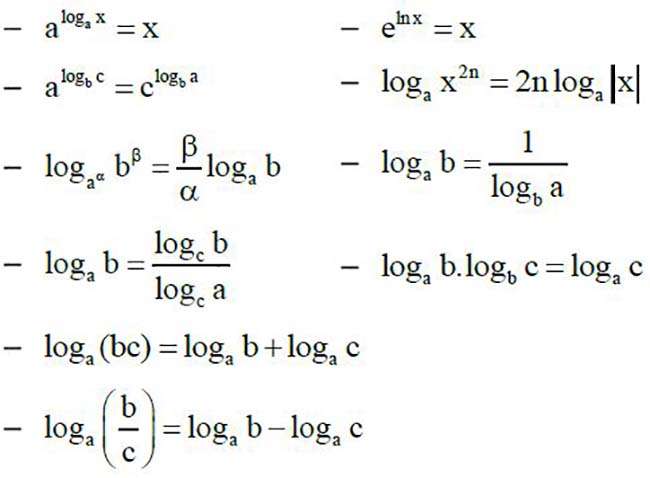
Toàn bộ chi tiết về công thức LOGARIT cần biết

Công thức Logarit là chủ đề quan trọng trong chương trình Toán ở bậc trung học phổ thông. Sau đây là toàn bộ chi tiết về công thức Logarit mà bạn cần biết để áp dụng và học tốt.

Logarit là gì?    

Logarit viết tắt là Log là phép toán nghịch đảo của lũy thừa. Theo đó, logarit của một số là số mũ của cơ số (giá trị cố định) nâng lên lũy thừa để tạo ra số khác. Một cách đơn giản, logarit là một phép nhân có số lần lặp đi lặp lại. Ví dụ: log_ax=y giống như a^y=x. Nếu logarit cơ số 10 của 1000 là 3. Ta có, 10³ là 1000 nghĩa là 1000 = 10 x 10 x 10 = 10³. Như vậy, phép nhân ở ví dụ được lặp đi lặp lại 3 lần.

Tóm lại, lũy thừa cho phép các số dương có thể nâng lên lũy thừa với số mũ bất kỳ luôn có kết quả là một số dương. Do đó, logarit dùng để tính toán phép nhân 2 số dương bất kỳ, điều kiện có 1 số dương # 1.

Bạn đang xem: Công thức log

Mẹo học logarit và bài tập ví dụ chi tiết

Để nắm chắc và áp dụng công thức logarit này vào làm bài tập toán, bạn cần hiểu rõ công thức Logarit và cách áp dụng. Sau đây là các bước giúp bạn hiểu thấu đáo về công thức logarit.

Biết được sự khác biệt giữa phương trình logarit và hàm mũ

Điều này rất đơn giản để nhận ra sự khác biệt. Một phương trình logarit có dạng như sau: log_ax=y

Như vậy, phương trình logarit luôn có chữ log. Nếu phương trình có số mũ có nghĩa là biến số được nâng lên thành lũy thừa thì đó là phương trình hàm mũ. Số mũ được đặt sau một số.

Logarit: log_ax=y

Số mũ: a^y=x

Biết các thành phần của công thức logarit

Ví dụ công thức logarit: log₂8=3

Các thành phần của công thức logarit: Log là viết tắt của logarit. Cơ số là 2. Đối số là 8. Số mũ là 3.

Biết sự khác biệt giữa các logarit

Bạn cần biết logarit có nhiều loại để phân biệt cho tốt. Logarit bao gồm:

• Logarit thập phân hay logarit cơ số 10 được viết là log₁₀b được viết phổ biến là lgb hoặc logb. Logarit cơ số 10 có tất cả các tính chất của logarit với cơ số > 1. Công thức: lgb=α↔10^α=b

• Logarite tự nhiên hay logarit cơ số e (trong đó e ≈ 2,718281828459045), viết là số logeb thường viết là lnb. Công thức như sau: lnb=α↔e^α=b

Ngoài ra, dựa theo tính chất của logarit, ta có các loại sau:

• Logarit của đơn vị và logarit của cơ số. Theo đó, với cơ số tùy ý, ta sẽ luôn có công thức logarit như sau: log_a1=0 và log_aa=1 

• Phép mũ hóa và phép logarit hóa theo cùng cơ số. Trong đó, phép mũ hóa số thực α theo cơ số a là tính aα; còn logarit số hóa dương B theo cơ số a sẽ tính logab là hai phép toán ngược nhau ∀a,b>0(a≠1) a^log_aα=logaaα=αaloga⁡α=log_a⁡a^α=α

log_ab^α=αlogabloga⁡bα=αlog_a⁡b

Logarit và các phép toán

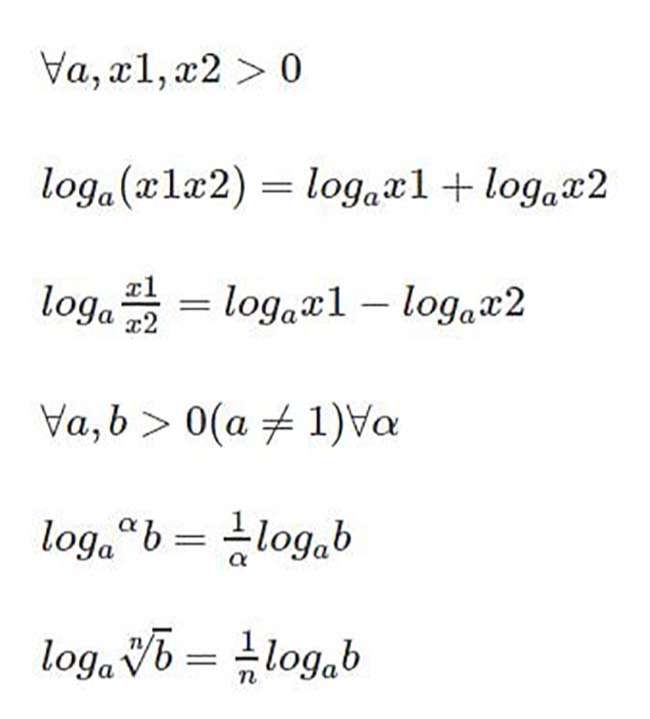
• Đổi cơ số cho phép chuyển các phép toán lấy logarit cơ số khác nhau khi tính logarit theo cùng một cơ số chung. Với công thức logarit này, khi biết logarit cơ số α, bạn sẽ tính được cơ số bất kỳ như tính được các logarit cơ số 2, 3 theo logarit cơ số 10.

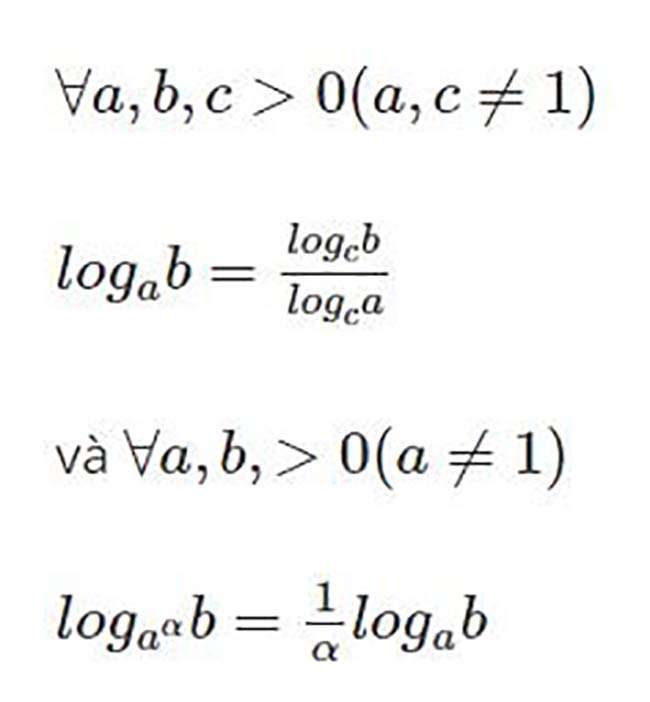
Biết và áp dụng các tính chất của logarit

Cho 2 số dương a và b với a#1 ta có các tính chất sau của logarit:

log_a(1)=0

log_a(a)=1

a^log_ab=b

log_aa^α=α

Tính chất của logarit giúp bạn giải các phương trình của logarit và hàm mũ. Nếu không có các tính chất này, bạn sẽ không thể giải được phương trình. Tính chất của logarit chỉ dùng được khi cơ số và đối số của logarit là dương, điều kiện cơ số a # 1 hoặc 0.

• Tính chất 1: log_a(xy)=log_ax+=logayloga⁡(xy)=loga⁡x+=log_a⁡y

Logarit của 2 số x và y nhân với nhau có thể phân chia thành 2 logarit riêng biệt bằng phép cộng.

Ví dụ: 

log₂16=log₂(8.2)=log₂8+log₂2=3+1=4

• Tính chất 2: log_a(x/y)=log_ax−log_ay 

Logarit của 2 số x và y chia cho nhau có thể phân chia thành 2 logarit bằng phép trừ. Theo đó, logarit của cơ số x sẽ trừ đi logarit của cơ số y.

Thực hành vào làm bài tập với các tính chất của logarit

Quy tắc tính logarit

Logarit của một tích

Logarit của lũy thừa

Ta có công thức logarit như sau: log_ab^α=α^log_ab điều kiện với mọi số α và a, b là số dương với a # 1.

Công thức logarit và cách giải nhanh

Về công thức logarit và cách giải nhanh, bạn sẽ cần quan tâm đến logarit hàm số lũy thừa, logarit hàm số mũ và hàm số logarit. Công thức tuy không khó nhưng dễ nhầm lẫn thiếu sót điều kiện khi làm nhiều dạng toán khác nhau. Chìa khóa để bạn làm tốt là học kỹ lý thuyết, hiểu chắc chắn các vấn đề sẽ giúp bạn tránh được điều này. Đồng thời ghi nhớ công thức logarit bằng cách làm bài tập lặp đi lặp lại nhiều lần và thử các dạng bài toán khác nhau.

Cách sử dụng bảng Logarit

Với bảng logarit, bạn sẽ tính toán nhanh hơn rất nhiều so với máy tính, đặc biệt khi muốn tính toán nhanh hoặc nhân số lớn, sử dụng logarit thuận tiện hơn cả.

Cách tìm logarit nhanh

Để tìm logarit nhanh, bạn cần chú ý các thông tin sau đây:

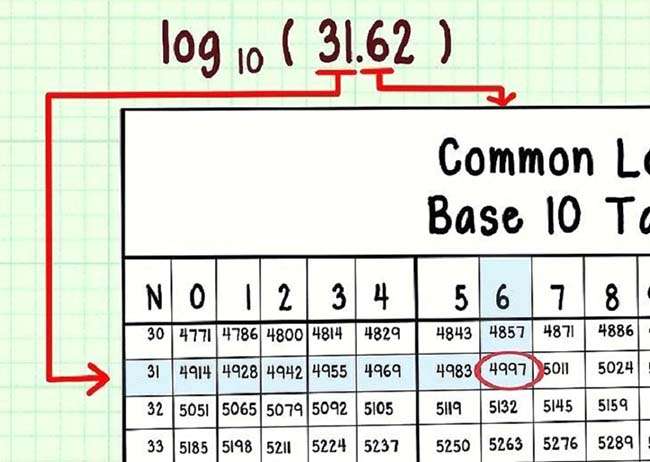
• Chọn bảng đúng: Hầu hết các bảng logarit là cho logarit cơ số 10 được gọi là logarit thập phân.

• Tìm ô đúng: Giá trị của ô tại các giao điểm của hàng dọc và hàng ngang.

• Tìm số chính xác nhất bằng cách sử dụng các cột nhỏ hơn ở phía bên phải của bảng. Sử dụng cách này trong trường hợp số có 4 hoặc nhiều hơn.

• Tìm tiền tố trước một số thập phân: Bảng logarit cho bạn biết tiền tố trước một số thập phân. Phần sau dấu phẩy gọi là mantissa.

• Tìm phần nguyên. Cách này dễ tìm nhất đối với logarit cơ số 10. Bạn tìm bằng cách đếm các chữ số còn lại của số thập phân và trừ đi một chữ số.

Cách tìm logarit nâng cao

Muốn giải những phương trình logarit nâng cao, bạn cần lưu ý những điều sau đây:

• Hiểu logarit là gì? Ví dụ, 10^2 là 100, 10^3 là 1000. Như vậy số mũ 2,3 là logarit cơ số 10 của 100 và 1000. Mỗi bảng logarit chỉ có thể sử dụng được với một cơ số nhất định. Cho đến nay, loại bảng logarit phổ biến nhất là logarit cơ số 10, còn gọi là logarit phổ thông.

• Xác định đặc tính của số mà bạn muốn tìm logarit

• Khi tra bảng logarit, bạn nên dùng ngón tay cẩn thận tra hàng dọc ngoài cùng bên trái để tính logarit trong bảng. Sau đó, bạn trượt ngón tay để tra điểm giao giữa hàng dọc và hàng ngang.

• Nếu bảng logarit có một bảng phụ nhỏ dùng để tính toán phép tính lớn hay muốn tìm giá trị chính xác hơn, bạn trượt tay đến cột trong bảng đó được đánh dấu bằng chữ số tiếp theo của số bạn đang tìm kiếm.

• Thêm các số được tìm thấy trong 2 bước trước đó với nhau.

• Thêm đặc tính: Khi tra ra điểm giao của hai hàng ra số cần tìm, bạn thêm đặc tính với mantissa ở trên để có kết quả tính logarit của mình.

Mẹo nhớ nhanh các công thức tính Logarit

Để nắm chắc kiến thức liên quan đến Logarit, các bạn có thể áp dụng 6 phương pháp sau đây:

• Nắm vững kiến thức nền tảng về Logarit, tham khảo tại Logarit đầy đủ và chi tiết nhất và bảng tổng hợp các công thức Logarit cơ bản
• Vì số lượng công thức nhiều như vậy, thì các bạn có thể sử dụng giấy nhớ để ghi lại các công thức và dán tại những vị trí trong nhà mà mình hay lui tới, đặc biệt là bàn học.
• Một cách phổ biến hơn là luyện tập, làm đi làm lại các bài tập trên lớp và làm thêm các bài tập trong sách tham khảo để nắm chắc kiến thức hơn, xem thêm các bài giải liên quan đến Logarit trong chương trình giải tích lớp 12

• Học nhóm và tham khảo ý kiến thầy cô sẽ giúp bạn hiểu sâu hơn về các kiến thức cơ bản và nâng cao của dạng bài tập.
• Tham khảo các video, bài giảng qua các trang mạng liên quan đến học tập, tại Cùng Học Vui
• Cuối cùng đừng quên bổ sung thêm kiến thức về các phần học khác để bổ trợ cho quá trình làm bài nhé.

[embeddoc url=”https://giasutamtaiduc.com/wp-content/uploads/2020/06/Công-thức-logarit-Công-thức-mũ.pdf” download=”all”]

Nâng cao kỹ năng giải toán trắc nghiệm 100% dạng bài mũ – logarit, số phức – Tô Thị Nga

Nội dung sách:
Chuyên đề 1. Mũ – Logarit
Vấn đề 1. Lũy thừa – Mũ – Logarit
+ Chủ đề 1. Lũy thừa – Logarit
+ Chủ đề 2. Hàm số mũ và hàm số logarit
Vấn đề 2. Phương trình mũ và logarit
Vấn đề 3. Bất phương trình mũ và logarit
1. Phương pháp đưa về cùng cơ số
2. Phương pháp mũ hóa, logarit hóa
3. Phương pháp đặt ẩn phụ
4. Giải bất phương trình mũ – logarit bằng phương pháp hàm số
5. Giải bất phương trình mũ – logarit bằng phương pháp đánh giá – bất đẳng thức
Vấn đề 4. Hệ phương trình và hệ bất phương trình mũ – logarit
+ Dạng 1. Giải hệ mũ – logarit bằng phương pháp biến đổi tương đương
+ Dạng 2. Giải hệ mũ – logarit bằng cách đặt ẩn phụ
+ Dạng 3. Giải hệ mũ – logarit bằng phương pháp hàm số
+ Dạng 4. Giải hệ mũ – logarit bằng phương pháp đánh giá bất đẳng thức
Chuyên đề 2. Số phức
Vấn đề 1. Số phức
Vấn đề 2. Các bài toán về biểu diễn hình học của số phức
Vấn đề 3. Tìm số phức có mô-đun lớn nhất, nhỏ nhất
Vấn đề 4. Căn bậc hai của số phức và phương trình căn bậc hai – Các phương trình quy về bậc hai – Hệ phương trình
Vấn đề 5. Dạng lượng giác của số phức

Link download sách

Đăng bởi: THPT Sóc Trăng

Chuyên mục: Giáo dục